What I've Learned About Teaching... Percentages with Ratio Tables

I've seen and read a lot about ratio tables and my initial attempts to use them started with year 8 percentages. They already had an idea of how to find basic percentages and an idea of FDP from year 7. I showed them a couple of different ways of visualising finding percentages of amounts, including dual number lines and ratio tables. We discussed which methods they liked and why. I was really surprised they liked the ratio tables, so I decided to stick with ratio tables to do some of the more complex percentage problems they needed to do and was surprised how universal they were for percentage problems, and how naturally multipliers come out of the method.

As with a lot of scaffolds, structures or manipulatives students need to be able to do the basics to be able to do more complex things later. You have to lay the foundations first! I would even go back and ensure they understand the principles of basic ratio tables before even introducing them in a percentages context. Ratio tables are a useful scaffold for many topics across the curriculum, and the more confident they are with the basics the easier they become in more difficult contexts. It is well worth investing time in the basics if you want to see the impact long term.

1. Basic percentages of amounts

I started with basic percentages of amounts to get students used to the structure and start the thinking about multipliers.

For example, find 40% of 80:

To set up the grid, I've always started with 100% in the top left box and the other percentage in the top right box. The bottom left box has the original amount/the full amount/100% in it, and then as we are trying to find 40% of 80, that is the box that is empty. There are then several ways of moving forward, depending on how confident your students are with multiplying decimals.

Highlighting the different methods and why they work is also useful at the beginning, so that students can use the ratio table more flexibly later on in the topic.

Method 1: Multiplying across

Students may need prompting and even practice before you start with the ratio tables of 100 x ___ = 40 to help them identify the multipliers more easily. They also seem to see multipliers when you highlight the equivalence between percentages and decimals, so a nudge of "what is 40% as a decimal?" will often get students the multiplier. After a bit of practice they generally get used to using the multipliers without too much thought, but if students are struggling they could try method 2 instead.

Method 2: Break it down to build it up

This may potentially be how they would do it traditionally, just in a more formatted way. This method would eventually lend itself to one step, as you may be able to guide students into seeing that dividing by ten then multiplying by 4 is the same as multiplying by 0.4.

Method 3: Multiplying down

This method is one I've found difficult to explain in the past without the use of ratio tables. The ratio tables really help to highlight this structure. It is sometimes easier to use this relationship, for example if it is a factor or multiple of 100 because students can either divide in one go or multiply in one go.

Now you might at this point be thinking, why use ratio tables for basic percentages of amounts when plenty of students can do so easily without - well the students need to understand how to use the structure and it actually helps if they have some prior knowledge to attach it to. Then they can go on to do more complex percentage questions. Depending on how quickly they pick up the basics, you can move on to other percentage questions so students can see the similarities and differences between the different types of questions.

I would use some carefully thought out questions, such as these to enable students to practice and to highlight what stays the same and what changes between each question:

Also discussing different methods and which is most efficient for each question or if there is anything surprising between the questions.

2. Percentage Increase and Decrease

Next I'd introduce percentage increase and decrease in a similar way. I again used dual number lines to help the visual of increasing by a percentage meaning we would end up with more than 100% and decreasing meaning we would end up with less than 100%. It is important students understand the percentage they are trying to find (e.g. a 20% increase will result in 120% of the original) to then use the ratio table.

Example: Increase 70 by 20%

Setting up the ratio table, again I always start with 100% top left with the full amount underneath, then the percentage I'm looking to find top right, in this case 120%. So now we find the gap using one of the methods below either in one step (preferable):

Or if students need to, in two or more steps:

In which case, you support students in aiming to get towards one step eventually as it is the most efficient way - particularly when students have a calculator. It is also quite nice to let students discuss how dividing by ten and multiplying by twelve is the same as multiplying by 1.2 and also dividing by 5 and multiplying by six. You can write them as fractions instead of decimals and really reinforce the importance and equivalence of FDP.

Some questions I might give students to practice and hopefully get them thinking:

3. Finding the original (100%) or Reverse Percentages

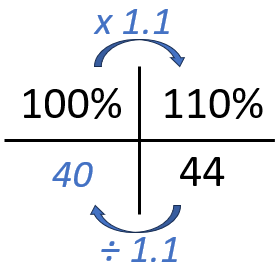
The cost of a train ticket increases by 10%. It now costs £44 for a return to Liverpool. How much did it cost before the price increase?

So in this question, we are given different information. Students may struggle initially working out what goes where in their table, but once they have the table filled in, it isn't a massive jump from increasing and decreasing by a percentage:

So the set up is different because this time, you are given that 110% is £44 in the question.

If students are confident with inverse operations, they can then use the fact they need to use inverse operations to find 100%:

It is more difficult, but not impossible, to use the relationship downwards, but this is where students may need fluency converting between fractions, decimals and percentages, and fluency knowing dividing by 10 and multiplying by 4 can also be written as multiplying by 4 tenths:

And as with previous examples, you can break it down into stages:

Again, this is with the aim of eventually being able to do it using a single multiplier in one go.

I'd ask some questions such as the following to hopefully get students thinking whilst practicing:

4. Writing as a percentage/percentage change

You can also use the structure to write anything as a percentage or to find a percentage change.

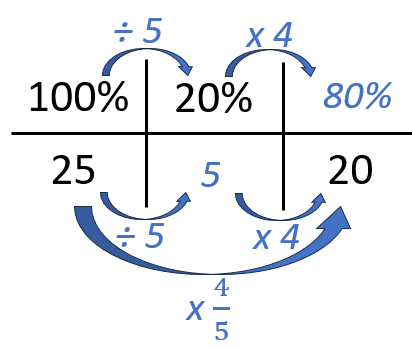
Example: Sally gets 20 out of 25 on her spelling test. What is her score as a percentage?

This time we are told 100% full marks is 25, the score is 20 so we need to find that as a percentage (top right corner). There are two ways of doing this one downwards:

As a bit of a bonus in terms of building connections, you can discuss why x by 0.25 or one quarter is equivalent to dividing by 4 and there is potential to bring in reciprocals.

Again, if needed split into steps which also can lend itself to relating the FDP equivalence again, and lends itself to discussing reciprocals:

Again, I'd give them some questions to practice whilst also trying to get them to reflect on similarities and differences:

And once they've done all the different types of questions, giving them some which I believe might count as 'same surface, different depth' to pull out the wording of questions and which is which type of question:

I'd also, from experience, ensure I show different contexts other than just money, so students see plenty of different contexts where percentages questions arise so they can apply the knowledge more flexibly to different contexts.

The students seemed to find the ratio tables really useful, as it was one structure to answer every type of question. They seem to more easily grasp multipliers as a concept and more naturally see when to divide by the multiplier. I really love how they highlight different relationships that other methods maybe wouldn't so easily lend themselves to. I am really looking forward to seeing how they will work beyond just percentages!